Ordnung schaffen - Graphen
Das Königsberger Brückenproblem
Die Stadt Königsberg (heute Kaliningrad), die vom Fluss Pregel durchflossen wird, ist durch ihn in mehrere Abschnitte geteilt, die durch sieben verschiedene Brücken miteinander verbunden sind (siehe Bilder). Der große Mathematiker Leonhard Euler versuchte 1736 zu klären, ob es einen Weg gibt, bei dem man alle sieben Brücken genau einmal überquert. Er interessierte sich dabei außerdem dafür, ob auch ein Rundweg möglich ist, bei dem man wieder zu seinem Ausgangspunkt zurückkommt. Gibt es diesen Weg oder nicht?
Euler zeigte, dass ein solcher Weg in Königsberg nicht möglich ist. Er abstrahierte dazu von der tatsächlichen geographischen Lage der Brücken und stellte das Problem als erster als sogenannten Graphen dar, für den er dann Regeln aufstellen konnte. (Graph unten) Er fand heraus, dass ein Rundweg der gesuchten Art genau dann möglich ist, wenn sich in keinem Knoten ( Uferplätze ) eine ungerade Zahl von Kanten ( Brücken) befindet. Damit war auch gezeigt, dass der Königsberger "Königsweg" ( Alle Brücken auf einem Rundweg genau einmal begehen ) nicht existierte. Zudem fand er heraus: Gibt es genau 2 Knoten mit einer ungeraden Anzahl von Kanten, dann existiert immer eine Route, die alle Kanten genau einmal enthält, aber Start- und Zielpunkt können dann nicht mehr identisch sein.
Aufgabe
Versetze eine der Königsberger Brücken so, dass der Rundgang möglich wird und zeichne das Ergebnis als Graph.
Das Problem des Handlungsreisenden
Das Problem des Handlungsreisenden (auch Rundreiseproblem, engl. Traveling Salesman Problem) ist ein weiteres berühmtes Problem, das man mit Hilfe von Graphen lösen kann Die Aufgabe besteht darin, eine Reihenfolge für den Besuch mehrerer Orte so zu wählen, dass die gesamte Reisestrecke des Handlungsreisenden nach der Rückkehr zum Ausgangsort möglichst kurz ist. Man zeichnet dazu einen Graphen, bei dem die Stationen der Reise als Knoten dargestellt werden und auf den Kanten der Weg oder die Reisezeit eingetragen wird. Beispiel:
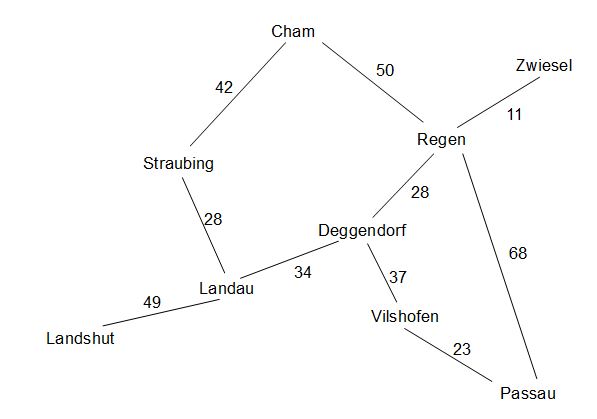
Aufgabe
Wie würde der günstigste Weg für einen Vertreter aussehen, der in Deggendorf wohnt und alle Orte auf dem Graphen an einem Tag besuchen soll?



